Методики измерения поверхностного натяжения неравновесных систем
Статьи
>>
Методики измерения поверхностного натяжения неравновесных систем
|
Измерение неравновесных/динамических поверхностных натяжений методом максимального давления пузырька известно уже много лет, в то время как измерение неравновесных натяжений с помощью уравнения Лапласа для висящих капель только недавно стало представлять интерес в связи с появлением более мощной вычислительной техники. Сравниваются три распространенных метода измерения поверхностного натяжения (метод пластин Вильгельми, метод висящих капель и метод максимального давления пузырька) для измерения неравновесных систем.
Метод пластин Вильгельми (реализуем на KRUSS K20 и KRUSS K100)
Метод пластин Вильгельми является наиболее известным методом измерения равновесных поверхностных натяжений жидких образцов. Маленькая пластина прикрепляется к датчику и погружается в жидкость, а затем извлекается до точки, где нижний край пластины точно параллелен поверхности объемной жидкости. В этот момент поверхностное натяжение связано с силой, оказываемой смачивающей его жидкостью, следующим уравнением:
δ – поверхностное натяжение
F – сила
θ - угол контакта образца
L- длина смоченной пластины
Почти для всех жидкостей относительно Pt θ = 0, поэтому уравнение упрощается до:
Несмотря на то, что метод пластин чаще всего используется для измерения равновесного поверхностного натяжения, для некоторых образцов метод пластины может быть использован для измерения неравновесного поверхностного натяжения. Например, зависящее от времени снижение поверхностного натяжения растворов, может быть легко измерено методом пластины, как показано ниже:
Если мы внимательно посмотрим на временную шкалу, мы увидим, что это чрезвычайно медленно адсорбирующаяся разновидность поверхностно-активного вещества. Ни один из растворов не пришел к равновесному поверхностному натяжению за 10 минут. Однако большинство интересных зависимостей от времени можно наблюдать в течение первых нескольких минут, которые можно легко измерить методом пластины.
Метод висящей капли (реализуем на KRUSS DSA 25)
Для этого метода каплю дозируют из шприца, пока она почти не отделится от кончика иглы. В этот момент делается снимок висящей капли, и контур профиля этой капли анализируется на предмет ее формы с помощью уравнения Лапласа.
Фактическая математика метода висящей капли основана на том факте, что существует разница давлений на изогнутых поверхностях. Перепад давления в любой заданной точке на поверхности (Δ P) равен средней кривизне поверхности в этой точке (1/r1 + 1/r2), где r1 и r2 - главные радиусы кривизны), умноженной на удвоенную величину натяжение (σ), содержащееся в поверхности.
Δ P = (1/r1 + 1/r2)·2·σ
Для висящей капли перепад давления внутри перепада между любыми двумя вертикальными положениями составляет:
Δ ρ·g·Z , где
Δ ρ - разница в плотности между жидкостью, образующей каплю, и объемным газом;
g - гравитационная постоянная;
Z - расстояние по вертикали между двумя положениями, как показано ниже.
Затем эти точки используются попарно с приведенными выше уравнениями для определения поверхностного натяжения. Таким образом:
Исторически уравнение решалось буквально путем фотографирования капли и выполнения математических расчетов позже, вручную и с помощью калькулятора. Сегодня с появлением современных компьютеров, уравнение решается гораздо проще. Фактически, в программе расчет выполняется для нескольких сотен пар точек менее чем за одну секунду. Такая скорость позволяет проследить изменение поверхностного натяжения (неравновесное поверхностное натяжение) в течение относительно коротких периодов времени:
Метод максимального давления пузырька (реализуем на KRUSS BP100 и KRUSS BPT)
Метод максимального давления пузырька является наиболее распространенным методом измерения динамического поверхностного натяжения. Во время измерения газ (обычно азот или воздух) выпускается через небольшую трубку с отверстием, которая погружается в исследуемый образец жидкости. Пузырьки, которые выдуваются из отверстия, имеют противодавление, необходимое для вытеснения их из трубки, и это противодавление связано с поверхностным натяжением следующей формой уравнения Лапласа:
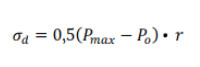 |
, где |
σd - поверхностное натяжение (динамическое)
r - радиус капилляра
Pmax - максимальное давление
Pο - гидростатическое давление
ρL - плотность жидкости
ρG - плотность газа
g - ускорение свободного падения
d - глубина капиллярного погружения
Таким образом, для любого заданного пузырька можно определить поверхностное натяжение интересующего раствора. Неравновесная составляющая эксперимента создается путем изменения скорости, с которой формируются пузырьки. При самых высоких скоростях образования пузырьков отводится меньше времени для накопления поверхностно-активного вещества на поверхности пузырьков, и, таким образом, достигается более короткий возраст поверхности. При низких скоростях образования пузырьков время накопления поверхностно-активного вещества на поверхности пузырьков увеличивается, и с помощью приведенного выше уравнения можно найти поверхностное натяжение при более длительном возрасте поверхности. Данные обычно отображаются в виде зависимости поверхностного натяжения от возраста поверхности:
На практике этот возраст поверхности может варьироваться от 5 мс до 1 минуты. Некоторые физические ограничения самого измерения не позволяют проверить возраст поверхности вне этих пределов.
Нулевой возраст поверхности
Нулевой возраст поверхности это та величина, под которой понимается устоявшаяся поверхность, когда на ней прекращают действовать другие силы, кроме поверхностного натяжения. Для метода пластины точный нулевой момент времени можно принять как точку, в которой пластина неподвижна. Обычно это происходит после любого перемешивания перед экспериментом. Хотя эта ситуация осложняется небольшим перемешиванием, которое происходит при погружении пластины в образец, мы будем предполагать, что нулевой момент времени наступает, когда перемешивание прекращается. В зависимости от используемой процедуры время между прекращением любого перемешивания и проведением первого измерения может составлять 5-30 секунд. Такая задержка и неточность нулевого времени допустимы. Для более короткого возраста задержка в измерении сама по себе перевешивает период измерения, что делает метод пластины бесполезным для измерения неравновесных напряжений более короткого старения. Время, необходимое для формирования новой, свежей висящей капли для последующего решения Лапласа неравновесного поверхностного натяжения, составляет примерно 0,2-2 секунды в зависимости от метода, использованного для создания капли. Эти более короткие временные рамки и точность нулевой точки обеспечивают большую точность в диапазоне измерения от секунды до минуты. Метод давления пузырька по своей сути точно определяет нулевой момент времени для новой, свежей поверхности. Нулевое время определяется как момент, когда продолжающийся пузырёк выходит из капилляра. Время между этой точкой и точкой измерения поверхностного натяжения точно определяется в режиме микросекунд. Этот точный нулевой момент времени позволяет получить точные кривые поверхностного натяжения вплоть до поверхностного возраста до 5 мс.
Какой метод выбрать?
Все 3 метода, описанные выше, сравниваются для очень распространенного поверхностно-активного вещества на основе этоксилата фенола на приведённой ниже кривой:
Фактически, данные о висящих каплях вступают в силу там, где метод давления пузырька достигает своего верхнего предела по возрасту поверхности. Данные пластины Вильгельми продолжаются в более длительных временных рамках, показанных методом висящей капли. По сути, обзор отвечает на вопрос, какой метод выбрать самостоятельно. Образцы, для которых требуется быстрый сбор данных и четко определенный нулевой момент времени, должны обрабатываться методом давления пузырька. Образцы, для которых не требуется такая скорость, могут обрабатываться, а в некоторых случаях должны обрабатываться методом висящей капли. Очень медленный поверхностный возраст и образцы, которые не изменяют свое поверхностное натяжение в течение минуты и более, все еще могут обрабатываться методом пластин Вильгельми.
Выводы
Тщательно выбирайте технику и инструменты, когда хотите получить данные о неравновесном поверхностном натяжении. В таблице мы привели примеры методов измерений для часто встречающихся неравновесных систем:
| ДАВЛЕНИЕ ПУЗЫРЬКА |
ВИСЯЩАЯ КАПЛЯ |
ПЛАСТИНА ВИЛЬГЕЛЬМИ |
| Кинетика основных ПАВ |
Вязкие чернила |
ТОЛЬКО для систем с очень медленно адсорбирующимися поверхностно-активными веществами. |
| Спреи |
Медленная адсорбция ПАВ |
| Быстрое нанесение покрытий |
Медленное нанесение покрытий |
|

