Определение поверхностной энергии материала
Статьи
>>
Определение поверхностной энергии материала
|
Свободная поверхностная энергия (энегрия поверхностного слоя) твердых материалов не может быть измерена непосредственно, она рассчитывается на основе краевого угла смачивания поверхности различными жидкостями. Основная задача при анализе свободной энергии поверхности – правильно подобрать тестовые жидкости и метод расчета, чтобы получить максимально достоверные результаты.
Иногда встречается формулировка “поверхностная энергия эмульсий”, что не совсем корректно, поскольку эмульсия представляет собой систему “жидкость-жидкость”, а поверхностная энергия – это характеристика твердых тел. К эмульсиям правильно применять понятие “межфазное натяжение”.
Как правило, для неполярных поверхностей используют неполярные жидкости и теории, которые не придают особого значения межмолекулярным взаимодействиям. Для полярных поверхностей, наоборот, применяются полярные жидкости и теории, основанные на взаимодействии активных центров (молекул) поверхности с газовой или жидкой фазой. Специалисты фирмы KRUSS обнаружили, что для измерения СЭП в качестве жидкости хорошо подходят водные растворы спирта, т.к. полярность раствора меняется при изменении соотношения вода : спирт. Но смеси жидкостей следует использовать осторожно, т.к. смачивание поверхности одним компонентом смеси может быть выше.
Ниже описаны несколько теорий, используемых в расчете данных в приборах для измерения краевого угла KRUSS. Предпочтения выбора той или иной теории остается за пользователями. Обращаем Ваше внимание, что все эти методы расчета реализованы в программном обеспечении ADVANCE фирмы KRUSS. Программа ADVANCE имеет интуитивный интерфейс, что позволяет легко работать даже начинающим пользователям приборов для измерения краевого угла KRUSS.
Метод Зисмана
Зисман предполагал, что свободная энергия твердой поверхности пропорциональна поверхностному натяжению жидкости, полностью смачивающей эту поверхность (т.е.  = 0°). По методу Зисмана строят график в координатах cos = 0°). По методу Зисмана строят график в координатах cos  (ось Y) - (ось Y) -  (ось Х) для различных жидкостей и далее экстраполируют усредненную кривую до cos (ось Х) для различных жидкостей и далее экстраполируют усредненную кривую до cos  = 1, полученное значение = 1, полученное значение  и является критическим напряжением сдвига. и является критическим напряжением сдвига.
В основном теория Зисмана великолепно работает на неполярных поверхностях (полиэтилен, полипропилен). Но для полярных поверхностей (стекло, керамика и металлы) теория Зисмана неадекватна, т.к. она основана на однопараметрической модели. Полимерные поверхности, которые подвергались термообработке или обработке плазмой, как правило, будут содержать полярные центры. Кроме того, существуют полярные полимеры (с гетероатомами), например, полиамиды, полиэфиры, полиакрилаты, поликарбонаты и др. В этом методе игнорируются межмолекулярные взаимодействия между жидкостью и твердым телом, а они очень сильны для полярных веществ.
Метод ОВРК (метод Оунса, Вендта, Рабеля и Кьельбле)
Оунс, Вендт, Рабель и Кьельбле рассматривали поверхностное натяжение с точки зрения полярной и дисперсной составляющих. Они представили, что энергия поверхностного слоя твердого тела включает две составляющие: дисперсионную и полярную. Дисперсионная составляющая включает силы Ван-дер-Ваальса и другие неспецифические взаимодействия, полярная составляющая – сильные взаимодействия и водородные связи. На основе этих представлений было выведено уравнение.
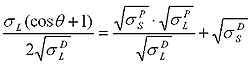
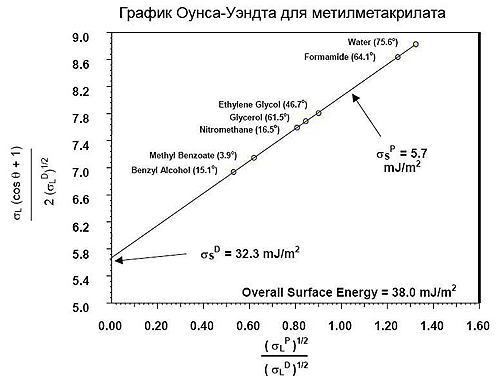
Для расчета по модели ОВРК кроме поверхностного натяжения жидкости и краевого угла, необходимо знать дисперсионную и полярную составляющие. Для определения полярной и дисперсионной составляющих жидкости используют поверхность с известными данными, например, тефлон (PTFE). Предполагается, что СЭП чистого тефлона 18.0 мДж/м2, и у него нет полярной составляющей. Значения полярной и дисперсионной составляющей для некоторых жидкостей имеются в литературе, а также в базе данных программ KRUSS. Зная составляющие жидкости, можно определить составляющие исследуемой твердой поверхности.
Метод Фоукса
Двухкомпонентная модель Фоукса также рассматривает полярные и дисперсионные взаимодействия, но с точки зрения адгезии. С математической точки зрения, теория Фоукса равнозначна теории ОВРК, но данное уравнение решается в два этапа.
На первом этапе определяется дисперсная составляющая СЭП с помощью неполярной жидкости (как правило, дийодометана CH2I2): т.к. у такой жидкости нет полярной составляющей, то уравнение упрощается и дает возможность рассчитать дисперсионную составляющую СЭП твердой поверхности.
На втором этапе уравнение решают относительно полярной жидкости (как правило, воды), для которой известны полярная и дисперсионная составляющие.
Двухкомпонентная модель Фоукса подходит для полярных поверхностей, но этот подход дает более высокие значения СЭП, чем по методу ОВРК. Построенная на основе изучения адгезии, модель Фоукса часто используется для изучения адгезионных свойств покрытий. Многие пользователи определяют СЭП по методу Фоукса, затем по методу Оунса-Уэндта, и по разности этих значений находят энергию адгезии (энергию сцепления между поверхностью и покрытием). Наибольшая адгезия будет наблюдаться, когда поверхность с большим процентом полярной составляющей будет смачиваться столь же полярной жидкостью.
Метод Фоукса (расширенный)
В расширенном методе Фоукса, кроме полярной и дисперсной составляющих свободной поверхностной энергии, рассматриваются водородные связи. В этом случае, решение уравнения проводится в три этапа: сначала с неполярной жидкостью, далее с полярной жидкостью, у которой отсутствуют водородные связи и завершается измерение на полярной жидкости с водородной составляющей.
Метод Ву
При исследовании межфазного натяжения Ву также начал с полярной и дисперсной составляющих. Однако в отличие от других исследователей, которые использовали в своих расчетах геометрическую прогрессию, Ву взял за основу среднегармоническое значение. В результате он достиг более точных результатов, в частности для систем с большой свободной энергией поверхности.
Для решения уравнения Ву необходимо как минимум 2 жидкости: полярную и неполярную. Для увеличения точности расчета поверхностной энергии можно увеличить количество жидкостей. В результате решения уравнения получаются две пары решений. Если одно из них имеет отрицательные значения, то выбор сделать не трудно, в противном случае необходимо свериться с результатами по другим методам расчета.
Метод Шультца
Данный метод используется только для поверхностей с высокой свободной энергией. Материалы с высокой энергией поверхности обычно хорошо смачиваются любыми жидкостями, поэтому их СЭП не может быть определена обычными методами. Для того чтобы исследовать такие системы, необходимо изменить обычную процедуру измерения: краевой угол («капли») измеряют в среде другой жидкости («среды») на или под поверхностью.
В методе Шультца-1 «капля» неизменна, а меняется окружающая фаза («среды«). В качестве «капли« обычно используется вода, в качестве окружающей среды – более легкая жидкость, которая не смешивается с водой.
В методе Шультца-2 «капля» – более легкая жидкость, чем окружающая среда. Капля находится под поверхностью и напоминает больше не «лежащую», а «висящую« каплю. В этом методе «среда« является постоянной жидкостью, а «капли» – различными. Преимуществом по отношению к методу Шультца-1 является то, что измеряемый краевой угол больше, а следовательно, выше точность.
Расчет свободной поверхностной энергии производится аналогично расчету метода Фоукса. Сначала производится расчет по неполярной жидкости, обладающей только дисперсионной составляющей, что позволяет определить дисперсионную составляющую поверхности. Далее уравнение решается для полярной жидкости, чтобы определить полярную составляющую поверхности.
Метод Оусса и Гуда
Оусс и Гуд также выделяли дисперсионную и полярную составляющие свободной энергии поверхности, но полярный компонент описывали с помощью льюисовых кислот и оснований. Таким образом, у них получалась трехкомпонентная модель: дисперсионная, кислотная и щелочная составляющие. Кислотная составляющая характеризует склонность поверхности при участии во взаимодействиях выступать в качестве донора электронов, а щелочная составляющая – в качестве акцептора электронов.
Для того чтобы решить уравнение Оусса и Гуда (определить 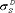 ) необходимы данные, как минимум, по трем жидкостям: ) необходимы данные, как минимум, по трем жидкостям: 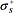 , , 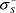 и краевой угол и краевой угол  . Как минимум две жидкости должны иметь кислотную и основную составляющие отличные от нуля. Кроме того, хотя бы одна жидкость должна иметь равные основную и дисперсную составляющие ( . Как минимум две жидкости должны иметь кислотную и основную составляющие отличные от нуля. Кроме того, хотя бы одна жидкость должна иметь равные основную и дисперсную составляющие (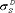 = = 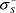 ), обычно для этих целей используют воду, т.к. она нейтральна по шкале Льюиса. ), обычно для этих целей используют воду, т.к. она нейтральна по шкале Льюиса.
Лабораторное оборудование от ГК «Тирит»
ГК «Тирит» специализируется на подборе и продаже лабораторного оборудования. В каталогах на нашем сайте Вы найдете широкий спектр современных приборов от ведущих европейских и американских производителей. ГК «Тирит» является эксклюзивным дилером в РФ немецкой компании KRUSS – лидера на рынке высокоточных измерительных приборов и аналитического оборудования. Наши технические специалисты помогут подобрать решение под задачи любой сложности, сопроводят запуск оборудования и проведут обучение персонала. Чтобы получить дополнительную консультацию и купить прибор –
позвоните по телефонам в Москве
+7 (495) 223-18-03,
8-800-600-18-03, напишите на почту
info@tirit.org или
заполните заявку на сайте.
|

